R语言实战|第16讲：预测模型中的变量筛选——基于Cox回归模型的代码实现与解析

本文接 预测模型变量筛选：方法篇

基因表达量高低分组的cox和连续变量cox回归计算的HR值差异太大? | 生信菜鸟团 (bio-info-trainee.com)

常见回归模型评估方法

平均绝对误差，Mean Absolute Error (MAE)：预测值与真实值之间平均相差多大；

均方误差，Mean Square Error (MSE)：是指参数估计值与参数真值之差平方的期望值。MSE是衡量平均误差的一种较方便的方法，MSE 可以评价数据的变化程度，MSE的值越小，说明预测模型描述数据具有更好的精确度。

R平方值，R-Squared (R²)：它是表示回归方程在多大程度上解释了因变量的变化，或者说方程对观测值的拟合程度如何。

其他

  RMSE：均方误差平方根；

  校正R²：对原始R²的改进：

  Cp：马洛斯CP值：

  AIC（赤池信息准则）和BIC (贝叶斯信息准则)

---

---

回归与判定标准

逐步回归，模型判定：AIC，值越小模型越优； 

全子集回归，模型判定，调整R²，值越大模型越优，BIC和CP值越小越好；

Lasso回归+交叉验证：模型判定，MSE，具体见下文。

目录

1. 单因素Cox初筛变量

2. 最优子集回归初筛变量

3. Lasso回归+交叉验证初筛变量

4. 三种方法筛选的变量纳入多因素Cox进行最终筛选

5. 用三种方法最终选出的变量构建模型并进行比较

6. 最佳的模型将用于构建预测模型Nomogram

本文筛选变量和建模思路

1.  三种方法筛选变量；

   1-1. 单因素Cox以P<0.05作为筛选变量的界限；

   1-2. 全子集回归以调整R²最大值判定最佳变量组合；

   1-3. Lasso回归+交叉验证以当均方误差(MSE)最小时对应的λ值来确定变量组合。

2.  三种方法筛选的变量纳入多因素Cox回归，采用逐步向后回归，以AIC最小值确定三种方法最终筛选的变量，构建模型。

3. 三种方法构建的模型以ROC曲线比较，选择AUC最大的作为构建列线图的模型。

注：本次使用的数据涉及小编的毕业论文数据，暂不公开分享，不过代码解释会尽量详细，使大家明白其中的含义。

载入R包和数据

#批量单因素回归分析包
library(survival)
library(plyr)#逐步回归包
library(MASS)#全子集回归包
library(leaps)#Lasso回归+交叉验证包
#library(survival)
library(glmnet)#多因素Cox模型ROC曲线比较包
library(riskRegression)
#library(survival)


#1.清理工作环境
rm(list = ls()) 
#2.数据放入工作目录后读取
aa<- read.csv(&＃39;预测模型变量筛选.csv&＃39;)


#3.查看变量名
names(aa)

#运行结果
# [1] "status" "time"   "age"    "t"      "n"      "hr"     "ki67"   "her2"  
# [9] "lvi"    "g"      "che"    "rt"     


#4.查看变量性质
str(aa)


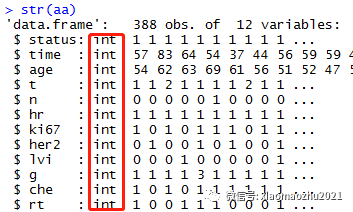
R语言默认数字为连续变量，但是我们12个变量中，只有时间和年龄是连续变量，因此在做数据分析前一定要将分类变量由数值（int/num）变为因子（factor），可以用for循环批量转换。

#5.批量数值转因子
for (i in names(aa)[c(1,4:12)]){aa[,i] <- as.factor(aa[,i])}


绿色部分是要转为因子的变量序号，我们选择第1列和第4-12列，数据为aa。

#6.再次查看变量性质，数据第1,4-12列变量已转为factor
str(aa)


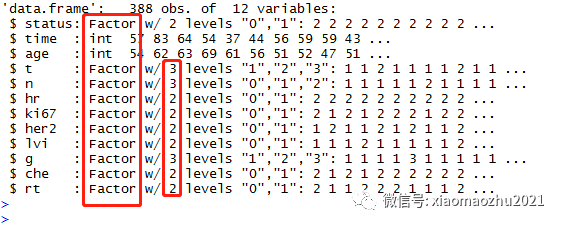
方法一：批量单因素筛选P<0.05的变量

代码来自：R语言|11. 超强的Table-2代码: 绘制任意数据的单因素合并多因素Cox回归三线表，这里只用代码前半部分。

#1.批量单因素cox的y
y<- Surv(time = aa$time,event = aa$status==0)
#2.循环函数
Uni_cox_model<- function(x){FML <- as.formula(paste0 ("y~",x))cox<- coxph(FML,data=aa)cox1<-summary(cox)HR <- round(cox1$coefficients[,2],2)PValue <- round(cox1$coefficients[,5],3)CI5 <-round(cox1$conf.int[,3],2)CI95 <-round(cox1$conf.int[,4],2)Uni_cox_model<- data.frame(&＃39;Characteristics&＃39; = x,&＃39;HR&＃39; = HR,&＃39;CI5&＃39; = CI5,&＃39;CI95&＃39; = CI95,&＃39;Uni_P&＃39; = PValue)return(Uni_cox_model)}  

#3.需要挑选需要进行单因素分析的变量。
variable.names<- colnames(aa)[c(3:12)];variable.names


#运行结果
#  [1] "age"  "t"    "n"    "hr"   "ki67" "her2" "lvi"  "g"    "che"  "rt" 


#4.进行循环并调整最终结果
Uni_cox <- lapply(variable.names, Uni_cox_model)
Uni_cox<- ldply(Uni_cox,data.frame)
Uni_cox$HR.CI95<-paste0(Uni_cox$HR," (",Uni_cox$CI5,&＃39;-&＃39;,Uni_cox$CI95,")")
Uni_cox<-Uni_cox[,-2:-4] 
View(Uni_cox)


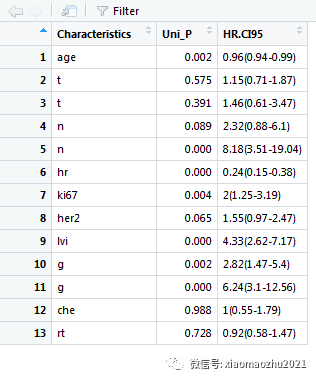
#5.筛选p<0.05的变量
Uni_cox$Characteristics[Uni_cox$Uni_P<0.05]


#运行结果
#  [1] age  n   hr  ki67  lvi  g  


结果：单因素Cox回归共筛选了6个p<0.05的变量：age+n+hr+ki67 +lvi+g

方法二：最优子集回归（全子集回归）

leaps<- regsubsets(status==0~age+t+n+hr+ki67+her2+lvi+g+che+rt,data = aa)
sum<- summary(leaps )


波浪号，左边为结局，右边为10个变量，regsubsets()函数进行全子集回归。

#按照最优子集回归模型评价标准找到最佳组合
which.min(sum$cp)#马洛斯CP最小值
which.max(sum$adjr2) #调整R2最大值
which.min(sum$bic) #贝叶斯信息准则最小值


结果：所有判断标准均汇报，6个变量是最佳组合。

以调整R²为标准画图，看变量组合

plot(leaps,scale="adjr2")


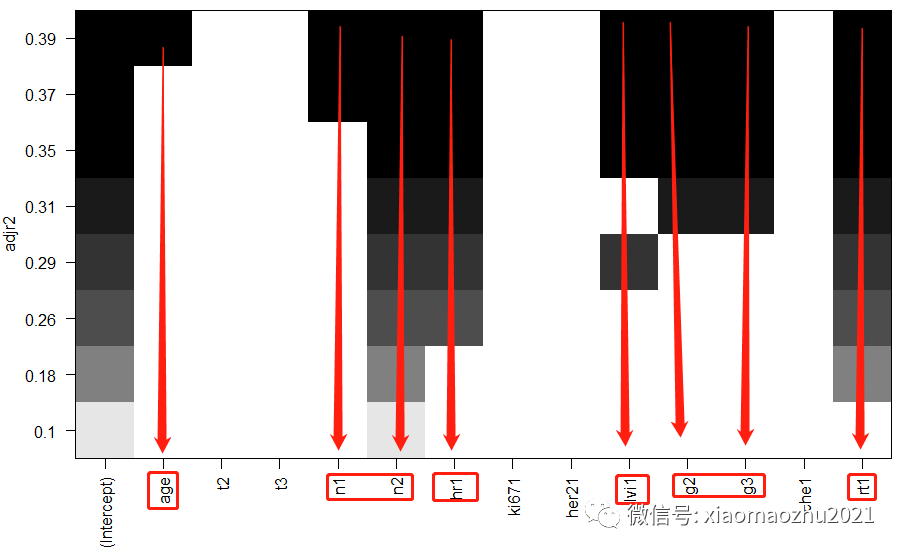
结果：最优子集回归（BSR, 全子集回归）筛选了6个变量age+ n+ hr+ lvi+ g+ rt

方法三：LASSO回归+交叉验证

注意：LASSO回归代码要求，

  1. 所有变量都为数字格式；

  2. 做lasso前必须将数据框变为矩阵，

即执行下面两行代码，x=要纳入的变量，y=生存分析的结局。这是代码报错的原因之一。

#1.数据转矩阵函数：data.matrix（）
x <- data.matrix(aa[,3:12])
y <- data.matrix(Surv(aa$time,aa$status==0))

#2.lasso回归
fit<- glmnet(x, y,family="cox",alpha=1)


参数 family 规定回归模型的类型 

family="gaussian" 适用于一维连续因变量，服从高斯分布，即正态分布，对应的模型为线性回归 

family="mgaussian" 说明因变量为服从高斯分布的连续型变量，但是有多个因变量，输入的因变量为一个矩阵，对应的模型为线性回归模型 

family="poisson" 适用于非负次数因变量，离散型变量，服从泊松分布，对应的模型为泊松回归

family="binomial" 适用于二元离散因变量，服从二项分布，对应的模型为逻辑回归

family="multinomial" 适用于多元离散因变量，对应的模型为逻辑回归模型 

family="cox" 说明因变量为生存分析中的因变量，同时拥有时间和状态两种属性，对应的模型为Cox回归模型

alpha=1：进行LASSO回归；

alpha=0，进行岭回归

#3.可视化结果
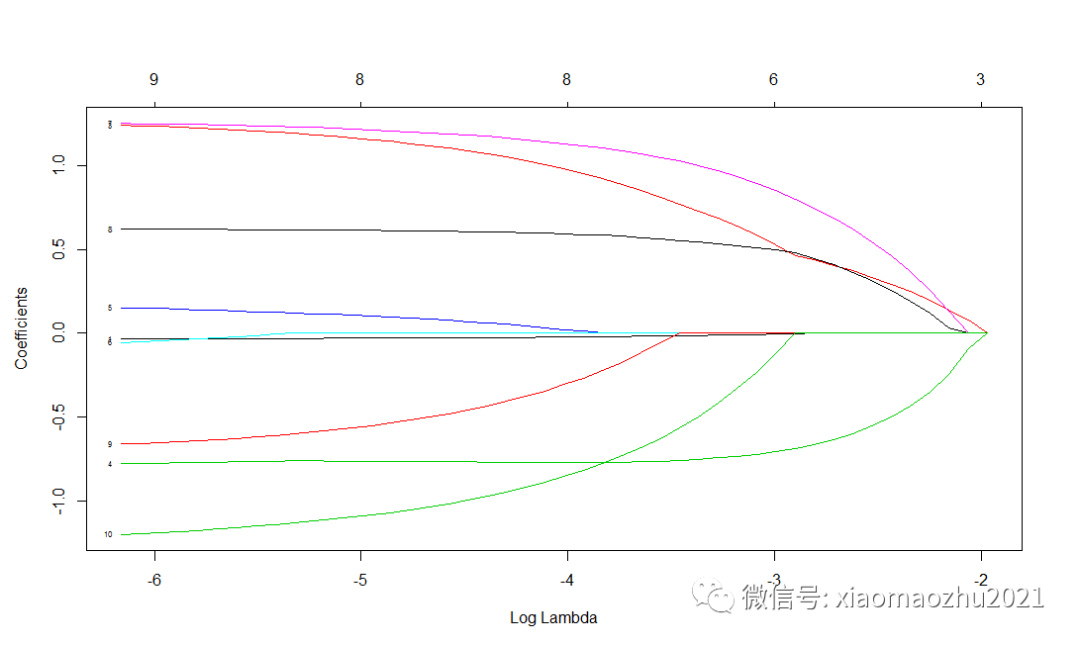
plot(fit, xvar="lambda", label=T)


图形结果解读：

LASSO为寻找最佳的模型，引入变量λ (lambda)【又叫收缩算子、模型系数比、调优系数或惩罚值】 

如图所示：随着λ增加，各变量的回归系数β在减小，有些会变为0，说明该变量在此时对模型贡献微乎其微，可以剔除。

图中，一条彩线代表一个变量的回归系数β值的变化，x轴下方的数字为惩罚值（调优系数），x轴上方为在该值下的剩余的变量个数。

LASSO 回归就是通过生成一个惩罚函数对回归模型中的变量回归系数进行压缩，达到防止过度拟合，解决严重共线性的问题。

所以，λ值确定决定了哪些变量可以使模型最优，使用交叉验证可寻找最佳λ值：当均方误差（MSE）最小时所对应的λ值决定纳入模型的变量。【MSE的值越小，说明预测模型具有更好的精确度】

#4.使用交叉验证来确定最佳的lambda。
cv.fit <- cv.glmnet(x, y,family="cox",alpha = 1)
plot(cv.fit)


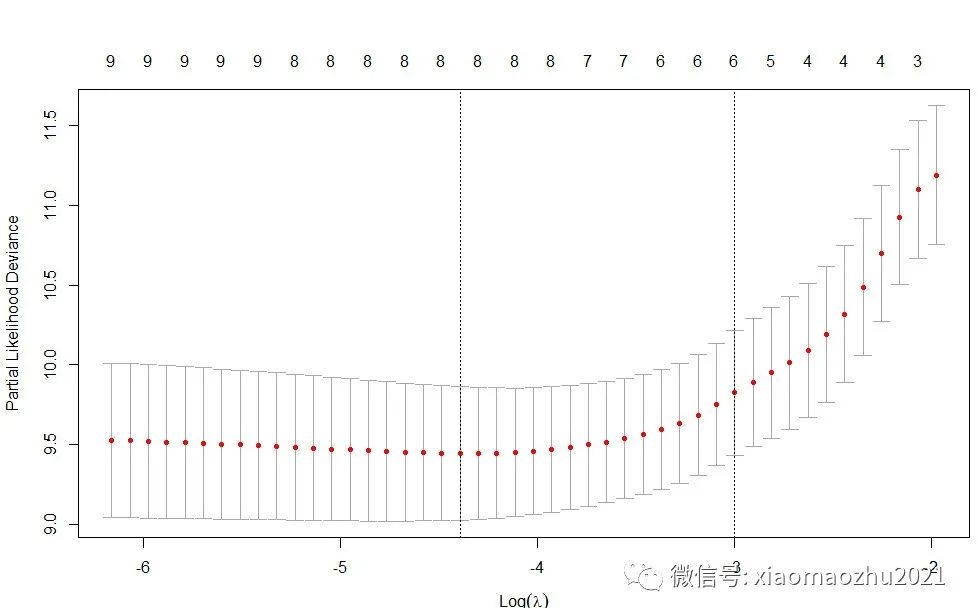
上图：Partial-likelihood deviance (偏似然偏差) 随Log(λ)变化曲线。

图中给出了两个惩罚值（调优系数）λ：

    一个是当MSE (均方误差) 最小时的λ值，即lambda.min； 

    另一个是在lambda.min值的一个方差范围内得到的最简单模型的λ值，即lambda.1se. 该值给出的是一个具备优良性能且自变量个数最少的模型，因此一般选择该值。

#5.显示两个惩罚值（调优系数）下的变量及其回归系数
ridge.coef1 <- predict(fit, s=cv.fit$lambda.1se, type = "coefficients");ridge.coef1
ridge.coef2 <- predict(fit, s=cv.fit$lambda.min, type = "coefficients");ridge.coef2


结果：lambda.min给出了8个变量；lambda.1se给出了6个变量。

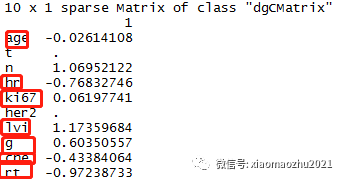
调优系数=lambda.1se：给出的是一个具备优良性能,且自变量个数最少的模型。因此LASSO回归给出的变量组合为6个：age+n+hr+lvi+g+rt

多因素Cox回归确定最终模型变量

总结

单因素Cox回归共筛选了6个p<0.05的变量: age+n+hr+ki67+lvi+g； 

最优子集回归根据调整R²最大值筛选了6个变量: age+n+hr+lvi+g+rt；

LASSO回归+交叉验证使用调优系数=lambda.1se给出了一个具备优良性能,且自变量个数最少的模型: age+n+hr+lvi+g+rt。

可以发现基于本数据，最优集回归和LASSO回归所筛选的变量是一样的。

下面将三种方法所筛选的变量组合分别纳入多因素Cox模型，使用逐步向后回归法以最小AIC值确定三种方法的最终模型。 

最后画出三个最终模型ROC曲线，以AUC值评估最佳模型。

1. 三种方法筛选的变量进行多因素Cox分析

#单因素cox筛选的变量进行多因素Cox，逐步向后回归法AIC最小值判断最终模型
COX<-coxph(Surv(time,status==0)~age+n+hr+ki67+lvi+g,data=aa,x=T)#6
stepAIC(COX,direction="backward")#全子集回归(BSR)筛选的变量多因素进行Cox，逐步向后回归法AIC最小值判断最终模型
BSR<-coxph(Surv(time,status==0)~age+n+hr+lvi+g+rt,data =aa,x=T)#6
stepAIC(BSR,direction="backward")#LASSO回归筛选的变量进行多因素Cox，逐步向后法逐步向后回归法AIC最小值判断最终模型
LASSO<-coxph(Surv(time,status==0)~age+n+hr+lvi+g+rt,data =aa,x=T)#6
stepAIC(LASSO,direction="backward")


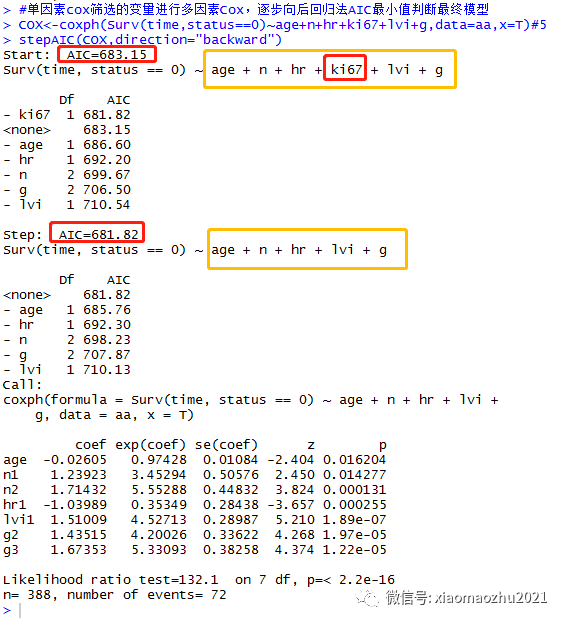
三个方法的多因素模型中只有单因素Cox所选的变量发生了剔除。

使用age+n+hr+ki67+lvi+g 构建的模型中，将ki67剔除后模型AIC值从683.15降至681.82。

因此由单因素Cox筛选的变量，最终建模变量为age+n+hr+lvi+g 5个变量，运行过程如下所示：

2. 三种方法构建的模型的比较 

#基于单因素Cox回归构建的最终模型，5个变量
COX1<-coxph(Surv(time,status==0)~age+n+hr+lvi+g,data=aa,x=T)#5#基于最优子集回归(BSR)构建的最终模型，6个变量
BSR<-coxph(Surv(time,status==0)~age+n+hr+lvi+g+rt,data =aa,x=T)#6#基于LASSO回归构建的最终模型，6个变量
LASSO<-coxph(Surv(time,status==0)~age+n+hr+lvi+g+rt,data =aa,x=T)#6


#绘制ROC曲线评估三种模型性能
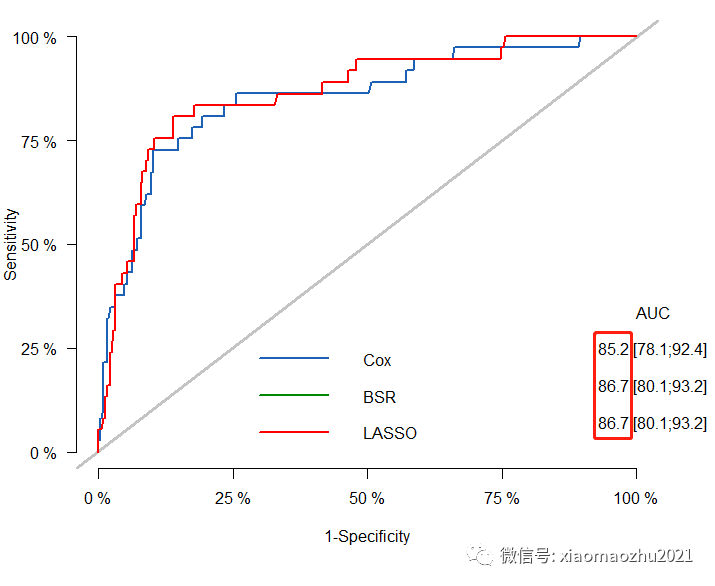
pk <- Score(list(model1 =COX1,model2 =BSR,model3 =LASSO), Hist(time, status==0)~1, data = aa,times =36, plots = &＃39;ROC&＃39;,metrics =c("auc", "brier"))plotROC(pk, col=c("#1c61b6", "#008600","red"),legend=c("COX", "BSR","LASSO"),lwd=2)


#模型AIC比较；AIC,越小越好
AIC(COX1,BSR,LASSO)


#运行结果
#         df   AIC
#  COX1   7 681.8188
#  BSR    8 663.8033
#  LASSO  8 663.8033


结果：

经比较，使用最优子集回归和LASSO回归筛选的变量所构建的模型更加优秀，其AUC值最大且AIC值最小。因此，基于本数据，最终选择age+n+hr+lvi+g+rt这6个因素构建Nomogram。

预测模型变量筛选的方法还有很多比如还可以用随机森林建模等，这里只对常见的方法做了简单介绍。但是，万变不离其宗，无论统计学方法再好，最最实用的还是基于临床意义选择变量建模。

之后将继续Nomogram模型构建与验证等，喜欢的小伙伴请点赞加分享支持一波，谢谢！